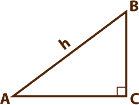
Un triangle rectangle : l’un des angles (ici, l’angle au point C) est un angle droit
Le Théorème de Pythagore
Le théorème de Pythagore dit, rappelons-le, que le carré de l’hypothénuse d’un triangle rectangle est égal à la somme des carrés des petites côtés.
Mais il est fort peu probable que Pythagore ait réellement découvert la démonstration de ce théorème, qui était connu des Babyloniens et, selon certains auteurs, Pythagore aurait vécu de nombreuses années à Babylone : c’est certainement de Babylone que le grand voyageur qu’était Pythagore a ramené cette "lumineuse égalité".
Un exemple de triangle rectangle, connu depuis des temps immémoriaux, est le fameux triangle "3-4-5", dont les trois côtés sont des nombres entiers, utilisé notamment par les constructeurs du Moyen-âge.
Utilité du théorème de Pythagore
Ce théorème a de nombreuses applications.
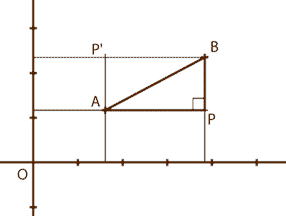
Il nous donne, par exemple, la distance entre deux points repérés par leurs coordonnées cartésiennes.
Comme la montre la figure ci-dessous, le segment qui relie deux points A et B peut être considéré comme l’hypothénuse d’un triangle rectangle dont le troisième côté est le point P.
Sa démonstration
En fait, on dénombre un grand nombre de démonstrations, de toutes époques et de toutes origines, de la Chine ancienne à la Maison Blanche.
Nous en avons choisi une, qui nous paraît être la plus ludique.
La démonstration est très simple et correspond bien à au génie grec (et rappelle étrangement la leçon de géométrie de Socrate) : elle passe par l’observation de différentes figures géométriques et ne nécessite qu’un minimum de connaissances.
Pour cette démonstration, nous allons nous inspirer d’un jeu chinois, le Tangram.
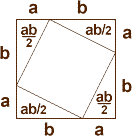
Nous allons découper des morceaux dans des carrés. L’hypothèse de départ est que si l’on enlève, à deux carrés identiques, des surfaces égales, quelle que soit la manière de les découper, les deux morceaux qui restent ont la même surface.
La figure qui servira à la démonstration est le carré de côté a + b. Si l’on découpe aux quatre coins de ce carré le triangle rectangle de petits côtés a et b, on obtient un second carré, de côté égal à l’hypothénuse (hypothénuse que l’on nommera "h" comme toute hypothénuse qui se respecte) du triangle rectangle. Et, donc, la surface de ce carré est égale au carré de l’hypothénuse.
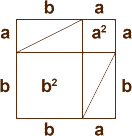
Dessinons à nouveau le carré de côté a + b (le "grand" carré), et découpons-le comme le montre la figure ci-contre : on obtient 2 carrés de côtés respectifs a et b, et deux rectangles de côtés a et b. On découpe ces deux rectangles en 4 triangles rectangles de petits côtés a et b, c’est à dire exactement le triangle dont on veut calculer l’hypothénuse.
On a dont ôté d’un même carré de côté (a + b) quatre triangles identiques de deux manières différentes, on peut donc affirmer que les surfaces restantes, d’une part le carré de côté h, d’autres part les deux carrés de côtés a et b, ont même surface, et la surface d’un carré est égale au carré de son côté, d’où :
h
Ce qu’il fallait démontrer.
La démonstration d’Euclide
Aux alentours de l’année 300 av. J.-C. parut un recueil qui allait avoir un retentissement considérable dans l’histoire des mathématiques en général et de la géométrie en particulier, les Éléments d’Euclide. Il y rassemble la somme de tout ce qui était connu des Grecs en matière de géométrie plane et en 3 dimensions (dont les solides platoniciens). La théorie des nombres y est également abordée.
Euclide a fait de son livre une somme, et il est certain que toutes les propositions qu’il cite n’ont pas été démontrées par lui, et peut-être en est-il ainsi de la démonstration qu’il donne de ce théorème. Ce qui n’ôte rien à la valeur de ces Éléments. Ils nous font toucher du doigt la manière très particulière qu’avaient les Grecs de raisonner, de "jouer" avec les mathématiques : très différente des "mathématiques modernes", héritières de la pensée arabe.
Et il est normal qu’Euclide expose dans ses Éléments le théorème de Pythagore et en fasse la démonstration.
Euclide s’appuie sur une étrange figure composée à partir du triangle rectangle :
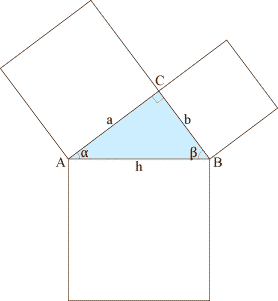
Au centre, le triangle, avec ses sommets A, B et C (en C, l’angle droit), les longeurs de ses côtés a, b et h ("h" pour hypothénuse) et ses angles α en A et β en B. Autour, les trois carrés dont un côté est, pour chacun, un côté du triangle. En bas, le "carré de l’hypothénuse".
Puis, on trace un certain nombre de segments entre certains angles, et l’on définit le point K, à la verticale du point A (à l’angle droit du triangle), sur la base du "carré de l’hypothénuse" :
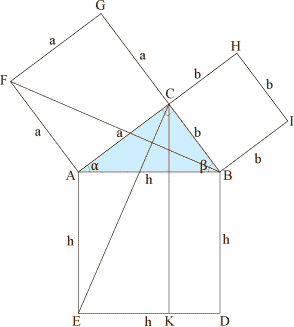
Ça commence à devenir passablement embrouillé : il va falloir élaguer. Mais tout est en place pour la démonstration.
Le raisonnement consiste à démontrer que le segment CK découpe le carré de l’hypothénuse en deux rectangles dont chacun est de même surface que l’un des deux autres carrés.
Revenons un peu en arrière, virtuellement, dans le livre d’Euclide. Il nous avait donné deux propositions (avec leur démonstration) préalables :

Illustration de la proposition 1

Illustration de la proposition 2
(1) deux parallélogrammes de même base et de même hauteur sont de même surface (en fait, Euclide ne parle pas de "hauteur", mais le "parallèles identiques"),
(2) la diagonale d’un parallélogramme le coupe en deux triangles de même surface.
Et rappelons qu’un parallélogramme est une figure à quatre côtés parallèles deux à deux. Un rectangle, un carré, un losange sont des cas particuliers de parallélogrammes.
Donc, regardons de plus près les triangles FBA et ABD :
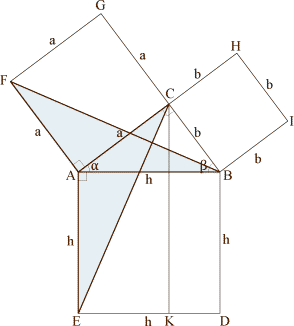
En fait, ces deux triangles sont identiques, parce qu’ils ont deux côtés et un angle égaux. Les deux côtés sont évidents : ils ont chacun deux côtés de longueurs respectives a et h. Pour l’angle, c’est celui qui est en B, et qui est la somme d’un angle droit et de l’angle du triangle rectangle objet de tous nos soins.
Donc, ces deux triangles sont égaux.
Or, ces deux tiangles sont chacun la moitié d’un parrallélogramme dont nous avons redessiné l’enveloppe en pointillés :
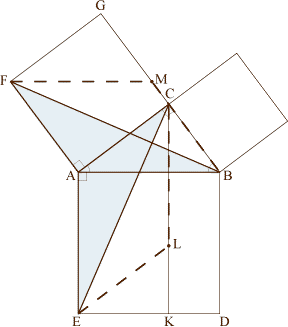
Prenons le cas du triangle ACE (triangle du bas) : on a défini un parallélogramme AELC en "doublant" le triangle ACE. Or, d’après la proposition (1), ce parallélogramme a même surface que la partie à gauche de l’axe CK du "carré de l’hypothénuse". Pourquoi ? Parce que ce parallélogramme et ce rectangle ont une base commune : le segment AE, et même hauteur EK (Euclide aurait parlé de même parallèles, les doites AE et CK. D’une manière exactement similaire, on prouve que le parallélogramme AFMB (défini sur le carré en haut à gauche) a même surface que le carré de côté a, le carré ACGF en haut à gauche.
Reprenons le raisonnement pour le petit carré et la portion du "carré de l’hypothénuse" qui nous avions laissée de côté, et nous trouvons bien que la somme des surfaces des deux carrés est égale à la surface du "carré de l’hypothénuse" :
h
Cette démonstration n’est pas la plus simple, et il paraît peu probable que les Grecs n’en aient pas connu d’autres. Mais elle s’inscrit dans l’ouvrage d’Euclide et découle de toutes les découvertes, grandes et petites, qu’Euclide avait regroupées dans le premier livre de ses Éléments.
Généralisation du théorème de Pythagore : la formule d’Al-Kashi
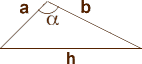
Si les philosophes-mathématiciens grecs s’attachaient à la beauté des cas particuliers, la logique des savants arabes s’orientait vers une approche globale : si le théorème de Pythagore s’applique aux triangles rectangles et seulement à ceux-ci, le mathématicien Al-Kashi, qui était actif à Samarcande au début du XVe siècle, a découvert la relation entre l’hypothénuse et les côtés de tout triangle :
h
où α est l’angle formé par les côtés a et b (angle opposé à l’hypothénuse). On appelle ce théorème, parfois, le "théorème de Pythagore généralisé"… mais il serait peut-être temps de rendre à César ce qui est à César, et de reconnaître aux Arabes, fondateurs des mathématiques modernes, les multiples avancées qu’ils ont réalisées dans de nombreux domaines scientifiques.
On peut confronter cette formule aux cas extrêmes :
– le plus simple, le triangle rectangle : l’angle est droit, donc égal à 90°, son cosinus est nul, ce qui nous donne la formule de Pythagore.
– le triangle est "plat" : soit il est entièrement ouvert (α = 180°, alors cosα = -1), soit totalement fermé (α = 0°, alors cosα = 1). Dans les deux cas, on retrouve la formule du carré de (a+b) ou de (a-b).
